Symmetric Balanced Laminate Abd

Balanced laminate typically when we just say balanced we mean w r t the in plane deformation a16 a26 0 and shear extension deformation is decoupled.

Symmetric balanced laminate abd. Makes analysis much simpler. The abd matrix below shows the stiffness coefficients for a specially orthotropic layup. Also sometimes called an anti symmetric laminate when unidirectional plies are used. Flexurally balanced is where d16 d26 0 and bend twist coupling does not exist.

A symmetric laminate is symmetric wrt to ply orientation above and below the laminate mid plane example 0 30 30 0 sometimes written 0 30 s is symmetric but not balanced balanced laminate is one where for every there is also a lamina example 0 30 30 30 30 0 or 0 30 30 s for a symmetric laminate b 0 always. If it is subjected only to moments it will have zero midplane strains. Calculate the laminate stiffness matrix. This is shown in.

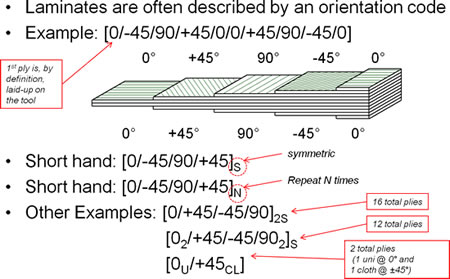
So whether you are designing or analyzing when examining the laminate simply compute the abd matrix for the desired laminate to quickly check if the a 16 and a 26 terms are zero note. To indicate symmetric laminates a contracted stacking sequence notation is used e g 0 90 45 s instead of 0 90 45 45 90 0 symmetric laminates are characterized by a specific feature. The same crack density has to be in both 90 layers located symmetrically with respect to the midplane. Laminate orientation code repeating groups of plies within a laminate can be placed in parentheses.

Notice that the a 16 a 26 and d 16 d 26 terms are indeed equal to zero regardless of the quantity or location of both the zero or 90 degree plies. Thermoelastic property degradation of symmetric and balanced laminates with arbitrary location of damaged 90 layers can be analyzed using eqns 12 17 12 22. Symmetric laminates if a symmetric laminate is subjected only to forces it will have zero midplane curvatures. Also prevents a laminate from twisting due to thermal loads.

Therein lies the answer to our first question concerning how one can quickly ascertain whether or not a laminate is balanced or not. However even in a damaged state the laminate has to remain symmetric. No fea is necessary at this point. In classical laminate theory the a b and d matrices collectively form the laminate stiffness matrix.

The rectangles highlight the extension shear a matrix and bend twist coupling terms d matrix. Their bending stiffness is higher than the bending stiffness of any asymmetric laminate composed of the same layers.